Anleitung: eine Fibonacci Spirale konstruieren und zeichnen

Sehr interessant ist es, eine Fibonacci Spirale (goldene Spirale) zu konstruieren und zu zeichnen. Dazu gebe ich heute eine entsprechende Anleitung. Wie gewohnt gebe ich gleich zwei unterschiedlich verschiedene Varianten, um dies zu veranschaulichen: die erste Variante ist ganz klassisch mit Zirkel und Papier. Die zweite Variante ist wieder auf digitale Art und Weise.

Hinweis: Wer eine einfachere „normale“ Spirale zeichnen möchte, der findet dazu eine Anleitung hier.

 

 

 

Anleitung: eine Fibonacci Spirale konstruieren und zeichnen mit Zirkel und PapierZu dieser Anleitung gibt es auch ein dementsprechendes Zeichenvideo auf YouTube:

 

Anleitung: eine Fibonacci Spirale konstruieren und zeichnen in digitaler Form

Wenn Du eine Fibonacci Spirale digital erstellen willst, dann hast Du gleich den Vorteil, dass der Platz zum Zeichnen nicht begrenzt ist. Allerdings möchte ich nicht in dieses Detail eingehen, wie man die passende Software dafür bedient. Zum Zeichnen empfehle ich generell Software, welche dafür ausgelegt ist. Beispielsweise ist OpenOffice Draw ganz geeignet, diese ist kostenlos erhältlich im Softwarepaket von OpenOffice.

Die Fibonacci Reihe

Die Fibonacci Reihe ist der ganze mathematische Hintergrund zur dieser Spirale. Diese mathematisch errechnete Zahlreihe ist unendlich: 0, 1, 1, 2 ,3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2585… usw.

Hinweis: Die Fibonacci-Folge habe ich hier weiter gerechnet. Des weiteren gibt es hier tiefere Zusammenhänge zur Fibonacci Folge.

Wer allerdings mehr darüber wissen möchte, kann sich z.B. hier weiter belesen.

 

Wie lässt sich die Fibonacci Reihe berechnen?

Das ist ganz einfach. Man fängt bei 0 + 1 = 1 an. Und dann schiebt man einfach die Rechensymbole, also das + und das = eine Stelle weiter. Nun steht 1 + 1 da, das ergibt 2. Das Schema wiederholt man, somit entsteht die Reihe. Es wird also beim nächsten Schritt einfach das = ersetzt mit dem +.

0 + 1 = 1 | 1 + 1 = 2 | 1 + 2 = 3 | 2 + 3 = 5  | 3 + 5 = 8 | 5 + 8 = 13 …

Dazu habe ich mal ein kleines GIF Bild gebaut, das eigentlich selbst erklärend sein sollte:

 

 

Große Fibonacci Spirale als Download gefällig?

Da die Größe der Fibonacci Reihe/Spirale nach außen kontinuierlich exponentiell zunimmt, ist es nur begrenzt möglich, jene darzustellen. Dennoch habe ich hier für Dich eine kleinere Spirale mal gezeichnet. Die kannst Du natürlich herunterladen und verwenden. Klicke einfach auf die Bilder, so bekommst eine große Auflösung:

 

Wenn Du eine Fibonacci Spirale als Vorlage oder Schablone direkt herunterladen und ausdrucken möchtest, so gibt es hier ein direkter PDF Download (klick aufs Bild):

 

 

 

 

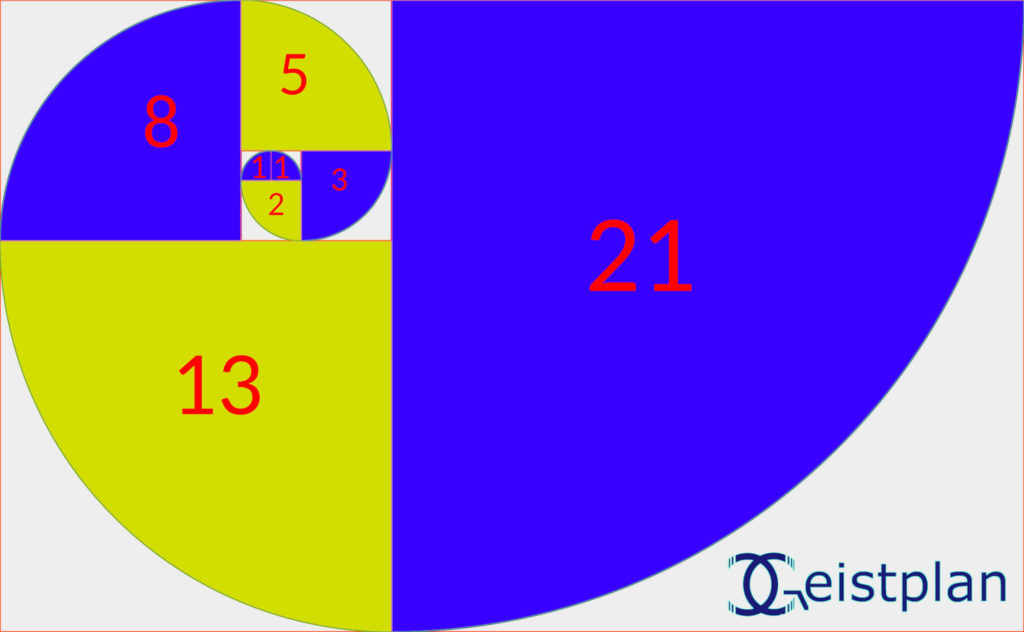
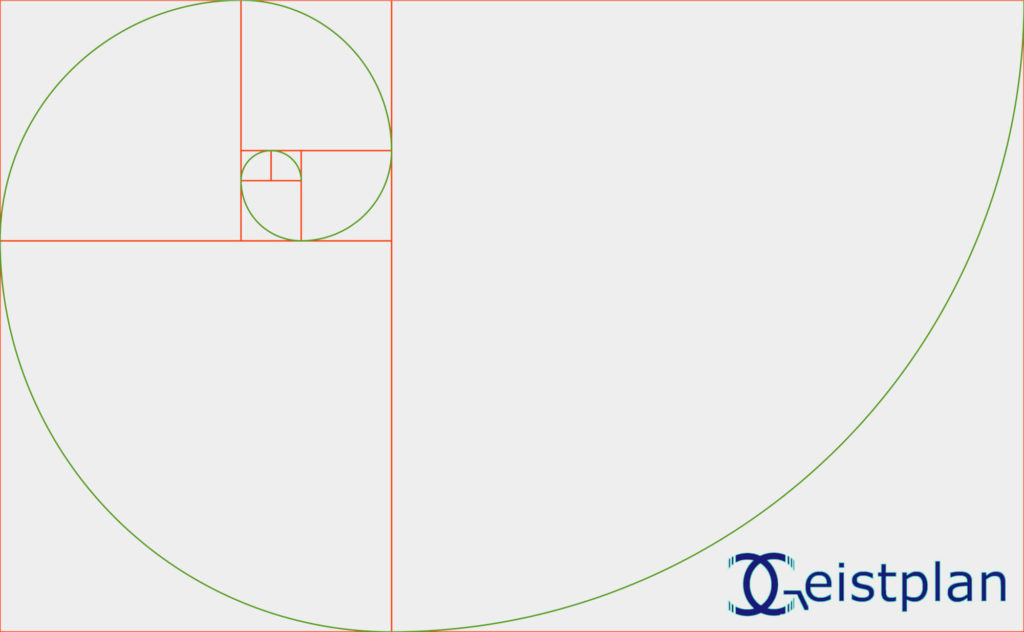
Übrigens: Die Venusblume besteht aus insgesamt 10 Fibonacci-Spiralen. Wenn Du also ein Fibonacci Mandala zeichnen möchtest, dann eignet sich die Venusblume gut dafür. Mit einem Klick auf das untere Bild gelangst Du zur Anleitung:

 

Der Goldene Schnitt in der Fibonacci Reihe

Fast jeder kennt die Kreiszahl PI mit 3.14… Aber schon einmal vom PHI gehört? PHI ist das männliche Gegenstück zu PI, denn es teilt ein Strecke in einem perfektem Verhältnis. Diese Zusammenhänge erläutere ich in diesem Beitrag, auch in diesem Beitrag gehe ich ansatzweise darauf ein, wo in unserem eigenem Körper die Naturkonstante PHI zu finden ist. Aber warum sollte ich soviel dazu texten, wenn es schon Blogs gibt, die es wesentlich besser machen? So schaue mal beispielsweise hier.

So, wie lässt sich nun der goldene Schnitt anhand der Fibonacci Reihe berechnen?

Das ist sehr spannend, finde ich. Denn nimmt man zwei aufeinander folgende Zahlen aus der Fibonacci Reihe und dividiert man die größere Zahl durch die kleiner Zahl, so erhält man die Naturkonstante PHI. Nun kommt aber der Witz an der Sache: Da auch diese Naturkonstante PHI wie PI unendlich viele Nachkommastellen hat, schafft man es niemals, es ganz genau auszurechnen. Allerdings je größer die Zahlen aus der Fibonacci Reihe sind, desto näher kommt man an PHI. Das haut mich wirklich vom Hocker! Nehmen wir mal beispielsweise zwei relativ kleine Zahlen aus der Fibonacci Reihe: 8 geteilt durch 5. So erhält man rund 1,67.

PHI ist allerdings 1,6180339.

Also nehmen wir mal zwei größere Zahlen aus der Fibonacci Reihe: 2585/1597=1,618659987. Faszinierend! Gerne könnt Ihr mal eine Tabelle machen und mal wirklich zwei große Zahlen gegeneinander dividieren. Je größer, desto genauer!

Lasst uns spielen!

 

Nun habe ich mal die obere Fibonacci Spirale genommen und horizontal, sowie vertikal gespiegelt. Hier das Resultat:

Jetzt noch ein Schippe darauf gelegt. Das obere Bild zwei dupliziert und übereinandergelegt. Fertig ist ein Mandala!

 

Wem kommt dieses Muster bekannt vor? Genau! Es ist das selbe Muster wie das negativ von einem Torus, oder wie der Samenstand einer Sonnenblume. In diesem Beitrag gehe ich entsprechend genauer darauf ein!

 

Daraus entstandene Mandalas:

 

Vielleicht ist allerdings die Fibonacci Spirale auch für die Hypnose gut geeignet 😉